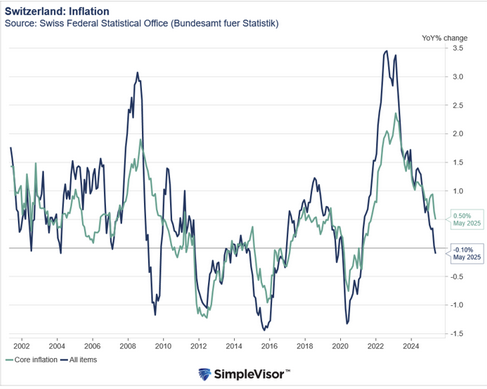
As of this morning, ABC’s Project FiveThirtyEight says that Donald Trump wins 53 times out of 100 and Kamala Harris wins 47 times out of 100. How can we make sense of this statement?
To do so, we have to understand the difference between case probability and class probability.
Presidential elections are unique events that are determined by the actions of humans, and so belong to the case probability category. The nature of such events is that numerical probabilities cannot be assigned in a scientific way to the possible outcomes. All we can do is guess, based on our own judgment of the circumstances and how we think the people who participate in determining the outcome will act. But this guess is a qualitative judgment and can only be articulated with numbers by recourse to metaphorical language.
The opposite kind of event, which we can make sense of using class probability, is one that is repeatable and not determined by human action—something like rolling dice or drawing a card from a shuffled deck. In these cases, numerical probabilities can be assigned. We know that a fair six-sided die will yield a particular outcome with a probability of one-sixth. We can roll it over and over again and discover these probabilities.
These two kinds of situations are categorically different. Ludwig von Mises said, “Case probability has nothing in common with class probability but the incompleteness of our knowledge. In every other regard the two are entirely different.” He discussed these two conceptions of probability because it has enormous implications for the way we do economics. Since economics deals with human action, quantitative methods like mathematical models or statistics are not suitable for developing economic theory or making sense of economic phenomena.
In the next section of chapter six of Human Action, Mises discussed various statements people might make regarding the outcome of a US presidential election:
On the eve of the 1944 presidential election people could have said:
(a) I am ready to bet three dollars against one that Roosevelt will be elected.
(b) I guess that out of the total amount of electors 45 millions will exercise their franchise, 25 millions of whom will vote for Roosevelt.
(c) I estimate Roosevelt’s chances as 9 to 1.
(d) I am certain that Roosevelt will be elected.
Statement (a) merely reflects one individual’s opinion about the outcome (and his “propensity for betting”). Statement (b) is also an opinion. Even though both use numbers to state the opinion, the numbers do not refer to numerical probabilities of the outcomes.
Mises says statement (d) is inexact:
If asked under oath on the witness stand whether he is as certain about Roosevelt’s future victory as about the fact that a block of ice will melt when exposed to a temperature of 150 degrees, our man would have answered no. He would have rectified his statement and would have declared: I am personally fully convinced that Roosevelt will carry on. That is my opinion. But, of course, this is not certainty, only the way I understand the conditions involved.
Statement (c) is the same kind of statement made by Project FiveThirtyEight and other election predictions based on simulations. Mises says that such statements are not scientific but are “metaphorical expressions.” They are using the language of statistics to express a judgment about an event that cannot be understood with statistics.
[Statement (c)] is a proposition about the expected outcome couched in arithmetical terms. It certainly does not mean that out of ten cases of the same type nine are favorable for Roosevelt and one unfavorable. It cannot have any reference to class probability. But what else can it mean?
It is a metaphorical expression. Most of the metaphors used in daily speech imaginatively identify an abstract object with another object that can be apprehended directly by the senses. Yet this is not a necessary feature of metaphorical language, but merely a consequence of the fact that the concrete is as a rule more familiar to us than the abstract. As metaphors aim at an explanation of something which is less well known by comparing it with something better known, they consist for the most part in identifying something abstract with a better-known concrete. The specific mark of our case is that it is an attempt to elucidate a complicated state of affairs by resorting to an analogy borrowed from a branch of higher mathematics, the calculus of probability. As it happens, this mathematical discipline is more popular than the analysis of the epistemological nature of understanding.
There is no use in applying the yardstick of logic to a critique of metaphorical language. Analogies and metaphors are always defective and logically unsatisfactory. It is usual to search for the underlying tertium comparationis. But even this is not permissible with regard to the metaphor we are dealing with. For the comparison is based on a conception which is in itself faulty in the very frame of the calculus of probability, namely the gambler’s fallacy. In asserting that Roosevelt’s chances are 9:1, the idea is that Roosevelt is in regard to the impending election in the position of a man who owns 90 per cent of all tickets of a lottery in regard to the first prize. It is implied that this ratio 9:1 tells us something substantial about the outcome of the unique case in which we are interested. There is no need to repeat that this is a mistaken idea.
You might question whether the election predictions that refer to numerical probabilities are really just metaphorical expressions of a judgment. Don’t they use sophisticated mathematical models to generate hundreds of simulated outcomes? Why aren’t the simulated outcomes like repeated laboratory experiments, meaning numerical probability can be assigned?
The issue is that both the construction of the model and the selection of data to put into the model involve judgments about what is relevant and the extent to which it bears on the outcome. If I collect a bunch of data about lemonade sales and the daily temperature, I might construct an equation that represents my best guess on how much lemonade will be sold tomorrow at a particular lemonade stand given tomorrow’s forecasted temperature. The formula will spit out a number, but this does not mean that the prediction is independent of my judgment. A machine does what it is designed to do just like a mathematical formula yields a particular outcome based on the way it is formulated.
In constructing the lemonade sales formula, I have to make a judgment about the effect of temperature on people’s desire to purchase lemonade and a judgment that other things are unimportant, like the day of the week, whether any large events are happening close to my stand that would increase foot traffic, and a host of other observable phenomena.
“Election simulations” therefore, are not a substitute for repeated experimentation and cannot be used to state class probabilities scientifically. There are two main reasons: (1) the formulas and inputs that produce the simulated outcomes represent the designers’ judgments, and (2) presidential elections are determined by human action, which is devoid of constant relations, meaning any historical pattern regarding polls and election outcomes, for example, cannot be assumed to hold in the future. Any statement that refers to numerical probability based on the outcome of such simulations must be interpreted as a metaphorical expression of someone’s opinion.
Full story here Are you the author? Previous post See more for Next postTags: Featured,newsletter